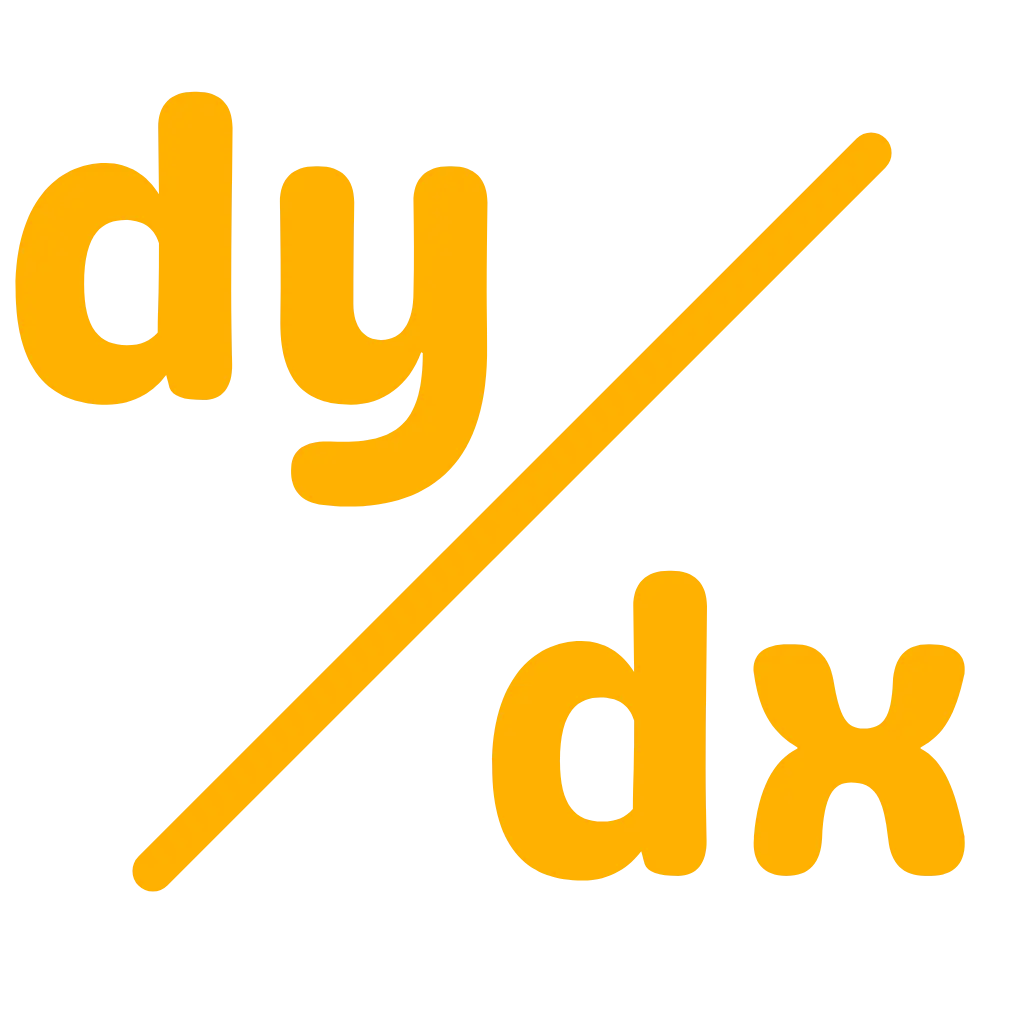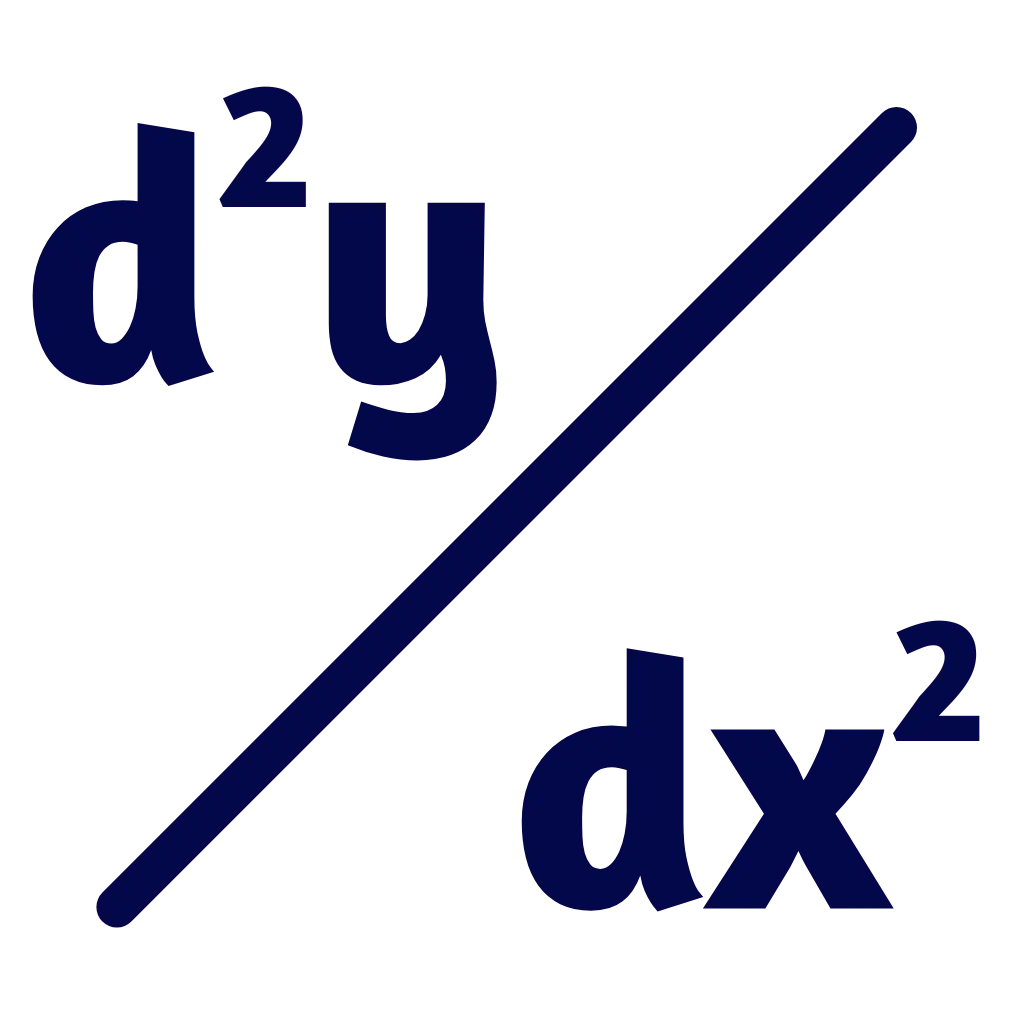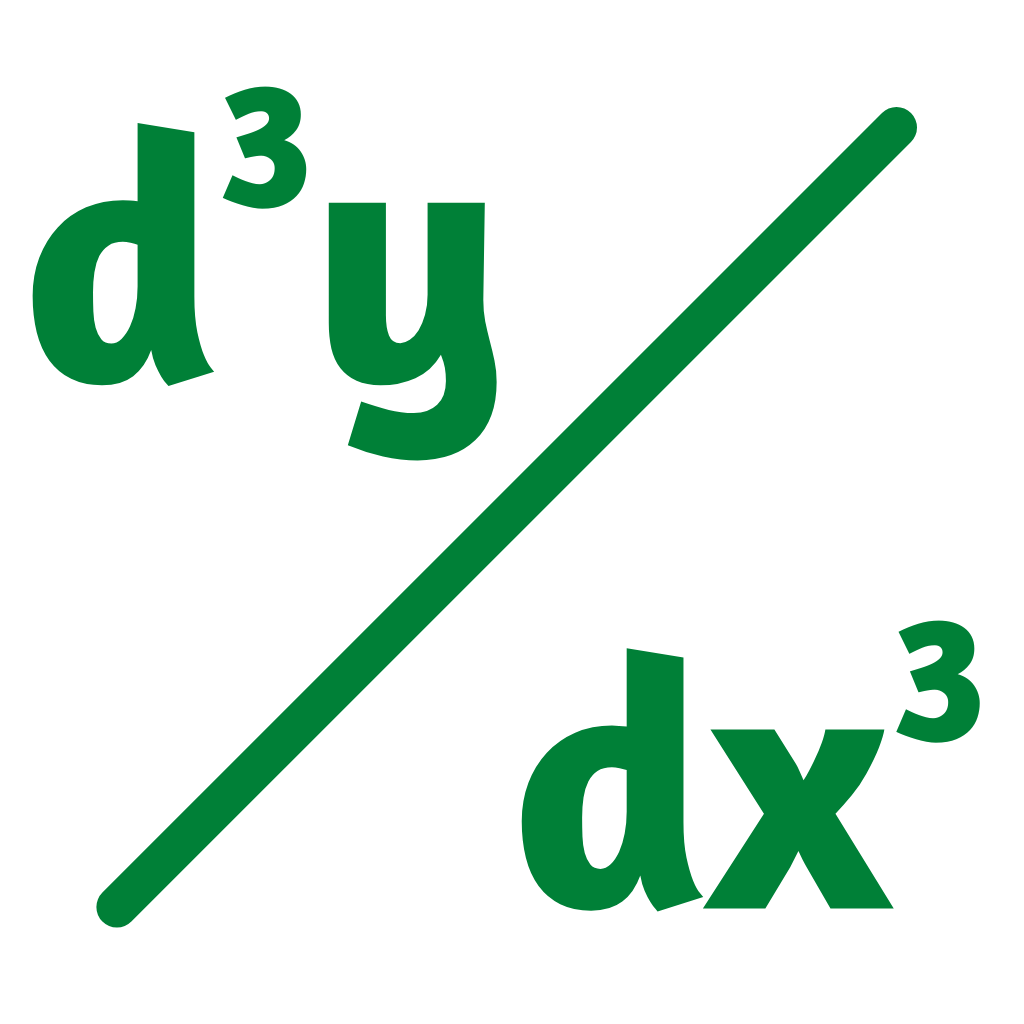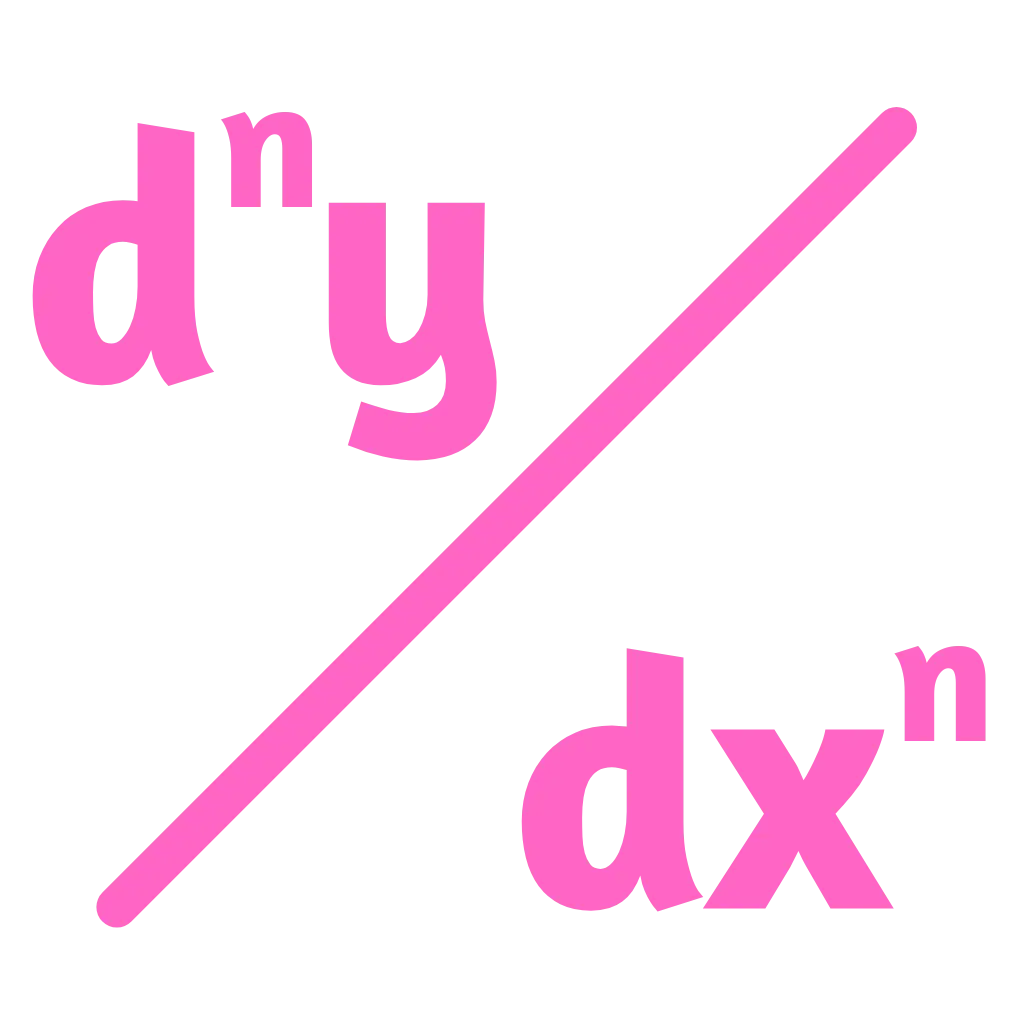nth Derivative Calculator

Introduction to the Higher Order Derivatives Calculator

The nth-order derivative calculator is a freely available online tool for calculating high-order derivatives. The higher order derivative calculator with steps tool is designed to find multiple derivatives of the function.

nth derivative calculator with steps

The higher order derivative calculator is a tool that calculates derivative according to the desire need of the user. It calculates the higher derivatives accurately and fast. The nth-order derivative calculator finds error-free results. Furthermore you can explore our powerful derivative at point calculator to instantly compute derivatives at specific points, simplifying complex mathematical tasks effortlessly.

What is the nth Derivative Calculator?

The higher derivative calculator is an online tool that calculates the derivative of any function nth times. Here nth means any higher-order number i.e. 1,2,3,...

An nth derivative calculator is a tool that takes higher-order derivatives i.e, when the derivative is taken for the first time it is called a 1st-order derivative and When the derivative is taken for the second time it is called 2nd derivative and so on. So, the nth derivative calculator calculates all the successive derivatives of a function.

Formula for the Higher Order Derivative Calculator

The nth derivative formula calculator is based on the basic rules of differentiation. To find the nth derivative of any function, you have to follow its basic pattern to reach the nth number derivative.

The following formula is used by the higher order derivatives calculator to find the nth derivative of the function.

$$ f^n (x) \;=\; \frac{d^n}{dx^n} [f(x)] $$

Let's see how to use this formula for the calculation of second derivative of a function.

Note: Click on this link to access a double derivative calculator that can assist you in solving for the second derivative of a function step by step and make it easy for you.

Example: Consider the function x^m to differentiate.

Solution: We have a function y = x^m

$$ f(x) \;=\; x^m $$ $$ f^n(x) \;=\; \frac{n!}{α^n} \int_0^1 f(x+αe^{2 \pi iz})e^{2 \pi iz} dz $$ $$ f^n(x) \;=\; \frac{n!}{α^n} \int_0^1 f(x+αe^{2 \pi iz})e^{2 \pi inz} dz $$ $$ f^n(x) \;=\; \frac{n!}{α^n} \left(_n^m \right) x^{m-n} α^n $$ $$ f^n(x) \;=\; \frac{n!}{α^n} \frac{m!}{n!(m-n)!} x^{m-n} α^n $$ $$ f^n(x) \;=\; m(m-1)...(m-n+1) x^{m-n} $$

How does the nth Derivative Formula Solver Work?

The nth-order derivative calculator is based on the rules of differentiation to find the nth derivative of the function.

Here is a function [f(x) = xn] whose first three successive derivatives are taken.

The first three derivatives of this function are:

f′(x) = nx^{n – 1}
f′′(x) = n (n – 1) x^{n – 2}
f′′′(x) = n (n – 1) (n – 2) x^{n – 3}

Steps for Working on this Calculator:

Following are the steps that are to be followed by the nth derivative calculator.
Open the calculator page, and load the function here in the required field.
Then select the order of derivatives from the drop-down list.
First of all, Enter all the values in the required input fields. Like variables, and other additional values.
After entering all the values in the required fields, now select any number in the “TIME” field that asks you how many times you want to differentiate the function.
Now just click on the “Compute” button. The nth derivative calculator will evaluate the slope of the tangent of the given function.
Finally, the results of your given differential results are displayed on your screen.
After evaluating the differential function, refresh the page for new calculations.

How to find a Higher Derivative Calculator with steps?

The following are the steps to be followed for finding the higher order derivatives calculator:

Step 1: Enter the keywords in the search bar of search engine like Google, Yahoo, Bing or Yandex.

Step 2: You can see some of the top results of your relevant query "nth derivative calculator" or "higher order derivative calculator".

Step 3: Hopefully, we will be in the top results of the SERP, you may recongnize us by https://derivative-calculators.com/.

Here it is, open the tool i.e. higher-order derivative calculator, put the required function and use it for the evaluation of your complex problems.

Importance of the nth Order Derivative Calculator

In mathematical calculations, using an online tool makes calculations easier. Before these tools, i.e (partial derivatives calculator, extreme points calculator and linear approximation calculator) the user has to do manual calculations, which seems to be quite hectic. So, these tools replace that hard exercise with some smart clicks.

Following is the list of some perks while using this nth-order derivative calculator:

The nth-order derivative calculator provides much ease to its users by giving them one-click calculations.
The user interface of the high derivative calculator tool is very friendly.
This higher order derivatives calculator gives you results in a fraction of a second.
It improves the analytical reasoning features of the user.
This nth derivative formula calculator has unlimited access the user can practice as many examples as he/she can.
The nth-order derivative calculator helps to find the derivative of the given function.
It makes accurate and reliable calculations without any errors.
This online tool is error-free and doesn’t charge any subscriptions from their users. This calculator has free unlimited access that is the user can do calculations multiple times.
The higher derivative calculator with steps gives the solution with step-by-step instructions.

Frequently Asked Question

How to Find the nth Derivative of a Function

To find the nth derivative of a function, the multiple derivative calculator uses the repeated differentiation of the functions that are n times. The general steps to find the nth derivative of the function are,

Start with the nth derivative function.
Now differentiate your function to determine the first derivative of the function. If you need to find out the second derivative then again differentiate.
For the nth derivative, you must be differentiating the function again and again n times.
Once you have derived the nth derivative, determine it at a specific point depending on the context of the problem.

What are Higher Order Derivatives

Higher-order derivatives are those derivatives that are differentiated more than one. It is generally calculated using the higher derivatives calculator. For example, if you have a function, then the function's first derivative will represent the function's rate of change.

If you differentiate the first derivative again, you will get the second derivative, which will be the rate of change of the changing function. When you continue this differentiation, you will get more derivatives.

Each higher-order derivative gives you information about the behavior of the function. Higher-order derivatives are used in calculus and many more fields to know about the behavior of the function.

What's the nth Derivative of sinx?

The nth derivative of function = sin(x)

$$ First\;derivative\;of\;sin(x) \;=\; cos(x) $$

$$ Second\;derivative\;of\;sin(x) \;=\; -sin(x) $$

$$ Third\;derivative\;of\;sin(x) \;=\; -cos(x) $$

$$ fourth\;derivative\;of\;sin(x) \;=\; cos(x) $$

The pattern repeats for every 4 derivatives in high order derivatives calculator. If n is a positive integer then the derivatives would be,

$$ n\; is \; divisible \; by \;4\; f^{(n)}(x) \;=\; sin(x) $$

$$ n\;leaves\;a\;remainder\;of\;1\;when\;divided\;by\;4: f^{(n)}(x) \;=\; cos(x) $$

$$ n\;leaves\;a\;remainder\;of\;2\;when\;divided\;by\;4: f^{(n)}(x) \;=\; -sin(x) $$

$$ n\;leaves\;a\;remainder\;of\;3\;when\;divided\;by\;4: f^{(n)}(x) \;=\; -cos(x) $$

So the nth derivative follows the periodic pattern according to the value of n.

Calculate the nth Derivative of sin^3x cos^2x?

To calculate the nth derivative of sin<3x cos^2x the complex derivative calculator uses the product rule. We will also use the product rule. So the given problem is,

$$ sin^3 x cos^2 x $$

$$ \frac{d}{dx} (sin^3 x cos^2 x) $$

Now apply the product rule,

$$ \frac{d}{dx} (sin^3 x cos^2 x) $$

The formula is,

$$ \frac{d}{dx} (f.g) \;=\; \biggr( \frac{d}{dx} f \biggr). g + f . \biggr( \frac{d}{dx} g \biggr) $$

Apply the above formula,

$$ sin^3 x \frac{d}{dx} (cos^2 x) + \biggr( \frac{d}{dx} (sin^3 x) \biggr) cos^2 x $$

Apply the chain rule,

$$ sin^3 x \frac{d}{dx} (cos^2 x) + \biggr(\frac{d}{dx} (sin^3 x) \biggr) cos^2 x $$

Replace the cos x with the u and apply the chain rule, replace u with cos x

$$ sin^3 x . 2cos^{2-1} x \frac{d}{dx} (cos x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

$$ sin^3 x . 2 cos^{2-1} x \frac{d}{dx}(cos x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

Subtract the numbers,

$$ sin^3 x. 2(cos x) \frac{d}{dx}(cos x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

Taking the derivative of trigonometric form,

$$ sin^3 x. 2(cos x) \frac{d}{dx}(cos x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

$$ sin^3 x . 2(cos x)(-sin x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

$$ sin^3 x.2(cos x)(-sin x) + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

$$ -2sin^4 x cos x + \biggr( \frac{d}{dx}(sin^3 x) \biggr) cos^2 x $$

$$ -2 sin^4 x cos x + \frac{d}{dx}(sin^3 x) cos^2 x $$

$$ -2sin^4 x cos x + 3 sin^{3-1}x \frac{d}{dx}(sin x). cos^2 x $$

Subtract the numbers

$$ -2sin^4 x cos x + 3sin^{3-1} x \frac{d}{dx}(sin x) . cos^2 x $$

$$ -2sin^4 x cos x + 3 sin^2 x \frac{d}{dx}(sin x). cos^2 x $$

$$ -2sin^4 x cos x + 3sin^2 x \frac{d}{dx}(sin x). cos^2 x $$

$$ -2sin^4 x cos x + 3 sin^2 x cos x. cos^2 x $$

Combine exponents,

$$ -2sin^4 x cos x + 3sin^2 x cos x cos^2 x $$

$$ -2sin^4 x cos x + 3sin^2 x cos^3 x $$

So the solution is,

$$ -2 sin^4 x cos x + 3 sin^2 x cos^3 x $$

Find the nth Derivative of (y) e^(2x)cos^(2)x sin x

You want to know how to find the nth derivative of a function given. To find the nth derivative of y = e^2x cos²(x) sin(x), we will use the product rule,

$$ y’ \;=\; (e^{2x})’ (cos^2 (x) sin(x)) + e^{2x}(cos^2(x) sin(x))’ $$

$$ y’ \;=\; 2e^{2x} cos^2(x) sin(x) + e^{2x}(-2 sin(x) cos(x) sin(x) + cos^2 (x) cos(x)) $$

$$ y’ \;=\; 2e^{2x} cos^2 (x) sin(x) + e^{2x}(-2 sin^2(x) cos(x) + cos^3 (x)) $$

Now determine the second derivative,

$$ y’’ \;=\; (2e^{2x})’ (cos^2(x) sin(x)) + 2e^{2x}(cos^2(x) sin(x))’ + (e^{2x}(-2sin^2(x) cos(x) + cos^3 (x)))’ $$

$$ y’’ \;=\; 4e^{2x} cos^2(x) sin(x) + 2e^{2x}(-2 sin(x) cos(x) sin(x) + cos^2(x) cos(x)) + e^{2x}(-4sin(x) cos^2(x) cos(x) - 2 sin^2(x) sin(x) - 3cos^2(x) sin(x)) $$

$$ y’’ \;=\; 4e^{2x} cos^2 (x) sin(x) + 2e^{2x} (-2sin^2(x) cos(x) + cos^3(x)) + e^{2x}( -4sin(x) cos^2(x) cos(x) - 2sin^3(x) - 3cos^2(x) sin(x)) $$

Continue this till you find the higher derivative.

Determine the e^x cos 2x nth Derivative

To determine e^x 2x, we will use the nth order derivative formula and then the product rule repeatedly:

$$ cos(2x) \biggr( \frac{d}{dx}(e^x) \biggr) + e^x \biggr(\frac{d}{dx}(cos(2x)) \biggr) $$

Using the chain rule,

$$ \;=\; e^x \biggr( \frac{d}{dx}(cos(2x)) \biggr) + e^x \biggr(\frac{d}{dx}(x) \biggr) cos(2x) $$

The derivative of x is 1 so,

$$ e^x \biggr( \frac{d}{dx}(cos(2x)) \biggr) + 1 e^x cos(2x) $$

$$ e^x cos(2x) + - \biggr( \frac{d}{dx}(2x) \biggr) sin(2x) e^x $$

$$ e^x cos(2x) - 2 \biggr( \frac{d}{dx}(x) \biggr) e^x sin(2x) $$

$$ e^x cos(2x) - 2e^x \biggr(\frac{d}{dx}(x) \biggr) sin(2x) $$

The derivative of the given x is 1 so,

$$ e^x cos(2x) - 1 (2e^x) sin(2x) $$

$$ e^x cos(2x) - 2e^x sin(2x) $$

$$ e^x (cos(2x) - 2sin(2x)) $$

Result:

More Calculators

Table of content

Buy Me a Coffee