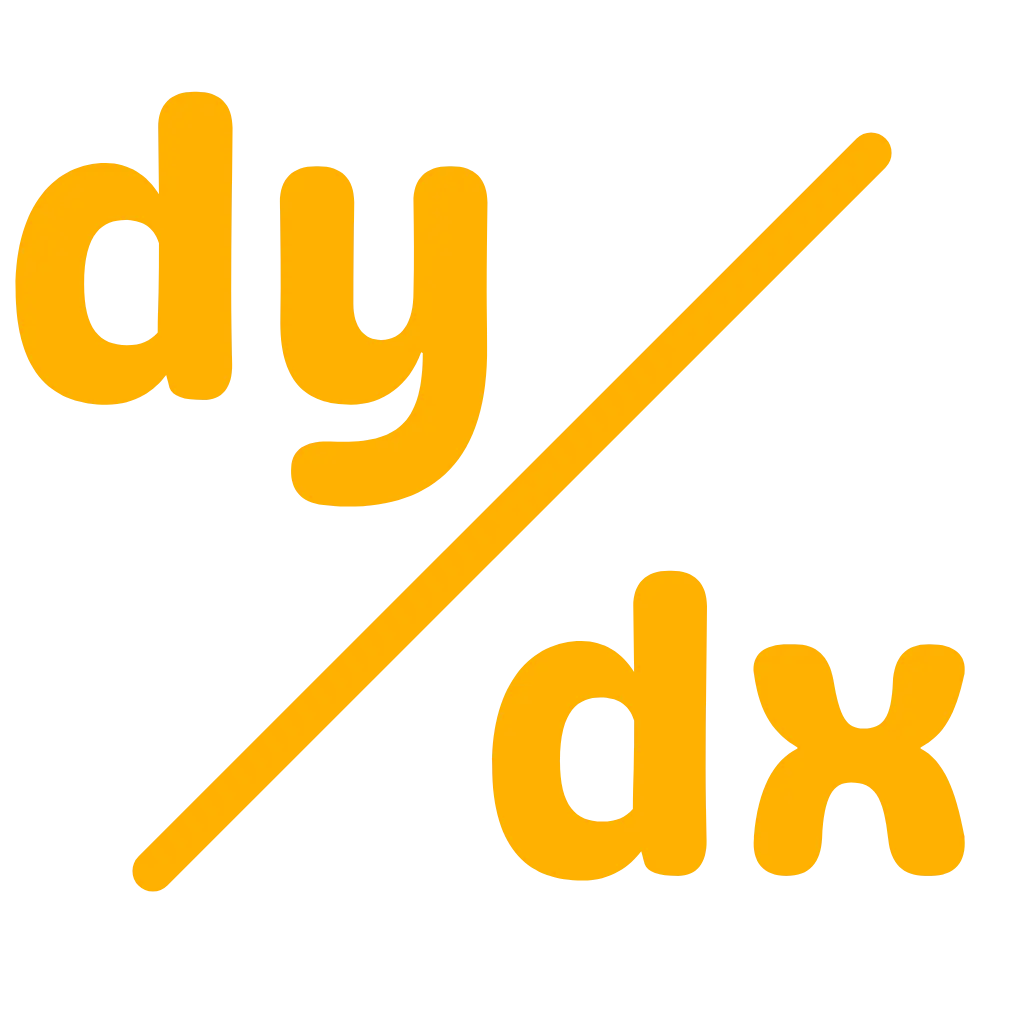Chain Rule Calculator

Introduction to the Composite Derivative Calculator

The chain rule multiderivative calculator is an online tool for finding the derivative of the given function using the chain rule method. This solver is a freely available online tool that calculates the derivatives in a fraction of a second.

chain rule calculator with steps

This composite function derivative calculator is free of cost without paying any subscription charges. This chain rule multivariable functions calculator saves precious time. Chain rule solvers have a user-friendly interface. It also shares common ground with the Product Rule and quotient of two functions calculator as they all deal with functions that involve multiple parts.

What is a Chain Rule Multivariable Calculator?

The chain rule derivative calculator is an online available tool for finding the derivatives of a given function. The chain rule calculator is used to find the derivative of two or more composite functions.

It finds it difficult to calculate the composite of two or more functions, so this composite function derivative calculator is introduced. This chain rule differentiation calculator calculates these functions by applying differentiation rules.

By following the differentiation rules, the constitution of two or more functions is calculated easily and accurately.

Note: Your journey doesn't end here. Check out our range of derivative calculators such as product rule calculator, normal line calculator and extrema calculator for various math tasks. Enhance your math skills effortlessly.

Formula Used by Chain Rule Derivative Calculator

The chain rule calculator with steps solves the constituent function of more than two functions with step-by-step guidance.

Sometimes, it is found difficult to solve a function that is composed of two or more functions. So, this chain solver uses the chain rule method and follows the differentiation rules to solve such composite functions.

Here is the formula that is used for the chain rule for the multiderivative function calculator.

$$ \frac{dy}{dx} \;=\; \frac{dy}{du} \cdot \frac{du}{dx} $$

By using this formula, our chain rule differentiation calculator make it easy to solve derivatives problems easy for it's users.

Let's see how our calculator perform calculation with the chain rule.

Example: Consider we have a function:

$$ G(x) \;=\; \left( \frac{2x-1}{3x+5} \right)^7 $$

Differentiate the function by using the chain rule of differentiation

$$ G'(x) \;=\; 7 \left( \frac{2x-1}{3x+5} \right)^6 \left( \frac{(3x+5)2-(2x-1)3}{(3x+5)^2} \right) $$ $$ G'(x) \;=\; 7 \left( \frac{2x-1}{3x+5} \right)^6 \left( \frac{13}{(3x+5)^2} \right) $$ $$ G'(x) \;=\; \frac{91(2x-1)^6}{(3x+5)^2} $$

In this way, our chain rule online tool performs calculation with possible intermediate steps and graphs.

How does Chain Rule Solver Work?

The chain rule calculator usually follows the following steps to calculate the composite derivative functions:

Step 1: Enter the composite function in the input bar. Or you can simply load the example from the drop-down list.

Step 2: Now select variable w.r.t to which you are looking for to differentiate the function. Select a varaible i.e. x,y,z or any other from the drop-down menu.

Step 3: After that, Now just click on the “Calculate” button. The chain solver will evaluate the composite functions.

Finally, that given function's derivatives and indefinite integrals will be displayed on your screen. After evaluating the function, refresh the page for new calculations.

How to find the Chain Rule Differentiation Calculator?

The composite derivative calculator is a very convenient tool for finding values for the given constituent function. Following steps should need to be followed for finding the multivariable function calculator:

First of all, Enter the keywords in the search bar of your search engine i.e. Google, Bing, Yandex or anyother you are using. Hopefully, you may find us in the top results of your search engine.
Secondly, if you are a regular user of these tools like linearization at a point calculator, we will recommend you to bookmark this website link on your browser named as online derivative calculator website.

Importance of Derivative of Composite Function Calculator

The chain rule for multivariable functions calculator is the best tool that is essential in differentiation. It is an important tool that is also used in physics as well as mathematics. Following are some benefits of users to differentiate the function with chain rule using this tool.

The chain rule calculator with steps gives you results in a fraction of a second. And this calculator gives the solution with step-by-step instructions.
The user interface of this online tool is very friendly.
This chain rule multivariable calculator is a freely available tool without any subscription charges.
By typing the simple keyword from your keyboard one can get this tool on his/her device.
This derivative of a composite function calculator determines the authenticity of the domain of the function, whether it is real or not.
The results of the composite function derivative calculator are authentic and reliable.
This calculator shows the graphical representation of the solution.

related: Moreover our derivative graphing calculator offers a graphical insight, making it easier to grasp the behavior of the derivative function.

Frequently Asked Question

What is the Chain Rule

Chain rule helps to determine the derivative of a composite function. It is a fundamental concept of calculus that helps to solve such complex functions.

For example, if there are two functions f(x) and g(u) and u is the function of x then the composite function h(x) = f(g(x)). This is given by,

$$ \frac{d}{dx} \biggr[f(g(x)) \biggr] \;=\; f’(g(x)) . g’(x) $$

The derivative calculator chain rule is solved using the chain rule. According to the chain rule to determine the derivative of a composite function first find the outer function’s derivative calculated at the inner function and afterwards multiply it by the inner function’s derivative concerning x.

How to Do Chain Rule

Here are some simple steps that are suggested by the composite functions calculator that will let you know how to do chain rules,

Identify the composite function first. That means one is the outer function and the other is the inner function. You have to identify both.

Starts by differentiating the outer function concerning its variable.
Now differentiate the inner function.
Combine the derivatives of inner and outer functions.

How would you Use the Chain Rule to Find dz/ dt

To find the chain rule of dz/dt, the chain rule step by step calculator follows the given steps:

Begin with the expression for z in terms of x and y
Now write the expression for x and y and express x and y as a function of t
Use the chain rule equation to differentiate:

$$ \frac{dz}{dt} \;=\; \frac{\partial z}{\partial x} . \frac{dx}{dt} + \frac{\partial z}{\partial y} . \frac{dy}{dt} $$

Now substitute the expressions x, y and z.
Calculate the 𝜕z/𝜕x and 𝜕z/𝜕y with the values of x and y. Also calculate the partial derivatives dx/dt and dy/dt using the expressions of x and y.
Enter the values into the chain rule formula and calculate.

What is the Limit Chain Rule

The limit chain rule is actually the alternative of chain rule which specifically deals with the limits. The limit of chain rule states that

“If the limit of f(x) as x approaches a exists, and the limit of g(x) as x approaches a exists, then the limit of the composite function f(g(x)) as x approaches a exists and is equal to the product of the limits of f(x) and g(x) as x approaches a.”

In mathematical form,

$$ if \;lim_{x \to a} f(x) \;=\; L_1 \;and \; lim_{x \to a} g(x) \;=\; L_2, \;then\; lim_{x \to a} f(g(x)) \;=\; L_1 . L_2 $$

This rule is helpful when we are calculating limits of composite functions from derivative calculator using chain rule. It helps you to break the limit of composite functions into the individual limits of the components.

Is there a Chain Rule for Integration

Yes, there is a chain rule for integration which is known as the integration by substitution or the chain in variables rule. This integration by substitution rule or change of variable rule is equivalent to differentiation and helpful in simplifying integrals by their substitutions which can also be simplified by differentiation calculator chain rule.

For using the chain rule for integration, following steps should be taken:

Take an integral that you want to simplify.
Identify if the integral involves a composite function or not.
Choose a variable that simplifies the integral
Now differentiate the chosen variable to find the derivative
Substitute the variable for the inner function
Now simplify the equation and integrate it
Once we are done with the integration, substitute it back the original variable.

Result:

More Calculators

Table of content

Buy Me a Coffee